|
| links |
| contact info | |
Discrete potentials and money
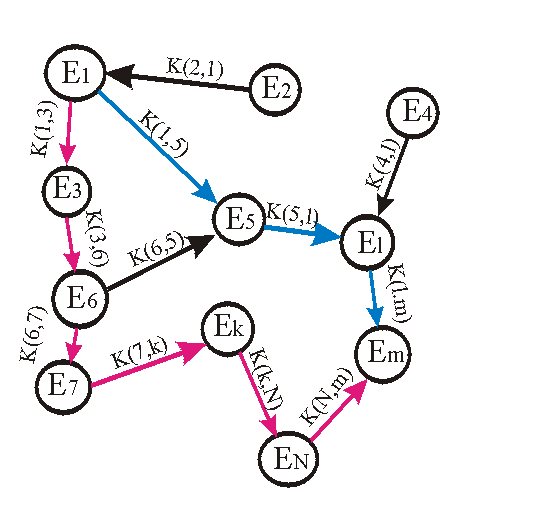
Let us consider a set of N elements E1 , E2 , E3 , ... , EN . With each ordered pair {Ep , Eq} of these elements a certain positive real number K(p,q) is associated. Some of these elements are shown on the picture as the graph's nodes, so their ordered pairs with corresponding numbers K(p,q) can be denoted by directed arrows. Now if we select an arbitrary directed chain{Ea , Eb , Ec , ... , Ep , Eq } of elements, we can assign a positive real number K(a,b,c, ... ,p,q) for this chain by the following simple rule:
K(a,b,c, ... ,p,q) = K(a,b)*K(b,c)* ... *K(p,q)
In other words, this number is a product of all numbers K for all pairs of elements which happened to be adjacent in the chain, directed from the chain's beginning to its end. On the pictures one chain is shown by red arrows and another chain by blue ones; to get K for the red chain, for example, one has to multiply K values for all red arrows. One can see, that in the general case the value of K depends on all elements of the chain, and not only on its first and last elements. Now we can give a
definition of discrete potential: a system of K values is called a potential (or discrete potential) system, if (and only if) for any two chains whose first elements are identical and whose last elements are identical their K values are equal. I.e., a system of K's is potential if K values do not depend on "path", but only on "starting and finishing points" of a chain. For example, if the system on our picture is potential, K(red) of the red chain must be equal to K(blue) of the blue one, as they both start with E1 and finish at Em. All natural features of potential systems appear here, such as K==1 for a closed chain, or K(a,b)==(K(b,a))-1 . Also, one can choose one of the elements -- Ebase for a reckoning point, and calculate K's for the rest of the elements with respect to this Ebase; value of K is now a function of element, but not of a chain. We can call this function potential P(En) , or just P(n) ; it is defined correct to multiplying by a factor, depending on the choice of Ebase. Value of K(a,b) for a pair {Ea , Eb} can be calculated by formula:
K(a,b) = P(b)/P(a)
Of course, instead of multiplying K values, we could have added them; then, if we demand independence of the result on the path of chain, we will get even more classic-like potential system, with chosen zero level, potential differences and zero "action" along closed chains. This is basically the same mathematical object, we can always substitute log(K') or exp(K'') of some other K' or K'' for K itself.
For our purposes multiplication case is more convenient, as it can model a situation with trading wares in society. Suppose our elements represent units of wares -- for example, E1 is a loaf of bread, E2 -- a liter of petrol, E3 -- an ounce of gold, and so forth. Let the K values represent barter exchange rates between these wares, i.e. rates of direct exchange without mediation of money. One can exchange wares by different ones in many steps, and the resulting rate for such a chain of exchange acts can be found by multiplying exchange rates for all steps.
Now common sense tells us that closed chain of exchanges is usually a pointless occupation, so really existing system of barter rates seems to be close enough to potential. Actually, one of the elements, such as the ounce of gold, was chosen to be the reckoning point; any other rate can be expressed through it to become so called price, which is nothing but value of the potential function P for a given unit of ware.
(Here we need to abstract from the fact that an exchange act itself costs something, too; so K for a closed chain would in practice be usually less then unity. This is similar to friction in otherwise potential system, where one must always produce positive work to move a body along a closed path. For gross trade with large lots, where expenses on exchange acts themselves are small compared to the worth of each lot, this abstraction can be adequate enough.)
But in practice we know some cases when people manage to gain by pure trade -- that is, they can find a closed chain of exchange acts, whose K value is more then one. Such a chain can be followed endlessly with a certain gain after every cycle. Vivid example is a currency exchange office, where the difference between buying and selling rates depends on current marketing conditions, rather then on the amount of labor needed for one exchange act. In the later case the difference would be constant and equal for all different currencies. So real system is not exactly potential, it contains some vortexes; nevertheless, money usually work. It seems to be this very speculative trade, that keeps the system close to potential -- if a vortex appear, some tradesman soon discovers it and starts to use to his profit; increased movement of wares along this chain shifts offer-demand balance for certain wares, altering barter rates, the whole thing working against the initial vortex. So real economies seem to work in a very peculiar regime, which can be called "quasi-potential": vortexes already exist, but money still work. The intensity of vortexes can serve as a criterion for stability of a monetary system; speculative trade is necessary to preserve potential system, where money can only work. On the other hand, as soon as potential system of barter rates was established and money prices became known, direct barter exchanges can become unnecessary -- it seems that they are not widely practiced in a developed economy. Whatever vortex appear, it can somehow be discovered and exploited just by watching differences in prices, without thinking of barter rates explicitly. So in some narrow limits a "quasi-potential" system can be maintained by watching "quasi-potentials" themselves; but beyond these limits it would collapse and would not be re-established without starting from the beginning with barter trade.
|
| links |
| contact info | |